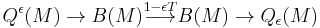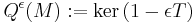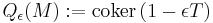ε-quadratic form

In mathematics, specifically the theory of quadratic forms, an ε-quadratic form is a generalization of quadratic forms to skew-symmetric settings and to *-rings; 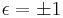$\epsilon = \pm 1$ , accordingly for symmetric or skew-symmetric. They are also called 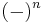$(-)^n$ -quadratic forms, particularly in the context of surgery theory.

There is the related notion of ε-symmetric forms, which generalizes symmetric forms, skew-symmetric forms (= symplectic forms), Hermitian forms, and skew-Hermitian forms. More briefly, one may refer to quadratic, skew-quadratic, symmetric, and skew-symmetric forms, where "skew" means 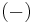$(-)$ and the * (involution) is implied.

The theory is 2-local: away from 2, ε-quadratic forms are equivalent to ε-symmetric forms: half the symmetrization map (below) gives an explicit isomorphism.

1 Definition
- 1.1 Generalization from *
2 Intuition
- 2.1 Refinements
3 Examples
4 Applications
5 References

Definition

ε-symmetric forms and ε-quadratic forms are defined as follows.^[1]

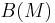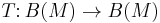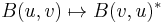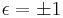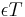Given a module $M$ over a *-ring $R$ , let $B(M)$ be the space of bilinear forms on $M$ , and let $T\colon B(M) \to B(M)$ be the "conjugate transpose" involution $B(u,v) \mapsto B(v,u)^*$ . Let $\epsilon=\pm 1$ ; then $\epsilon T$ is also an involution. Define the ε-symmetric forms as the invariants of 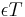$\epsilon T$ , and the ε-quadratic forms are the coinvariants.

As a short exact sequence,

$Q^\epsilon(M) \to B(M) \stackrel{1-\epsilon T}{\longrightarrow} B(M) \to Q_\epsilon(M)$

As kernel (algebra) and cokernel,

$Q^\epsilon(M)�:= \mbox{ker}\,(1-\epsilon T)$

$Q_\epsilon(M)�:= \mbox{coker}\,(1-\epsilon T)$

The notation 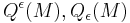$Q^\epsilon(M), Q_\epsilon(M)$ follows the standard notation 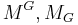$M^G, M_G$ for the invariants and coinvariants for a group action, here of the order 2 group (an involution).

We obtain a homomorphism $(1 %2B \epsilon T)\colon Q_\epsilon(M) \to Q^\epsilon(M)$ which is bijective if 2 is invertible in R. (The inverse is given by multiplication with 1/2.)

An ε-quadratic form 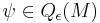$\psi \in Q_\epsilon(M)$ is called non-degenerate if the associated ε-symmetric form 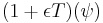$(1 %2B \epsilon T)(\psi)$ is non-degenerate.

Generalization from *

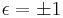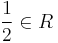If the * is trivial, then $\epsilon=\pm 1$ , and "away from 2" means that 2 is invertible: $\frac{1}{2} \in R$ .

More generally, one can take for 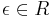$\epsilon \in R$ any element such that 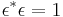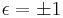$\epsilon^*\epsilon=1$ . $\epsilon=\pm 1$ always satisfy this, but so does any element of norm 1, such as complex numbers of unit norm.

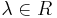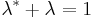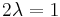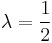Similarly, in the presence of a non-trivial *, ε-symmetric forms are equivalent to ε-quadratic forms if there is an element $\lambda \in R$ such that $\lambda^* %2B \lambda = 1$ . If * is trivial, this is equivalent to $2\lambda=1$ or $\lambda = \frac{1}{2}$ .

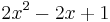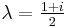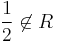For instance, in the ring $R=\mathbf{Z}\left[\textstyle{\frac{1%2Bi}{2}}\right]$ (the integral lattice for the quadratic form $2x^2-2x%2B1$ ), with complex conjugation, $\lambda=\textstyle{\frac{1%2Bi}{2}}$ is such an element, though $\frac{1}{2} \not\in R$ .

Intuition

In terms of matrices, (we take $V$ to be 2-dimensional):

matrices 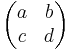$\begin{pmatrix}a & b\\c & d\end{pmatrix}$ correspond to bilinear forms
the subspace of symmetric matrices 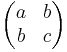$\begin{pmatrix}a & b\\b & c\end{pmatrix}$ correspond to symmetric forms
the subspace of (-1)-symmetric matrices 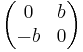$\begin{pmatrix}0 & b\\-b & 0\end{pmatrix}$ correspond to symplectic forms
the bilinear form 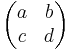$\begin{pmatrix}a & b\\c & d\end{pmatrix}$ yields the quadratic form

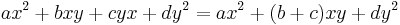$ax^2 %2B bxy%2Bcyx %2B dy^2 = ax^2 %2B (b%2Bc)xy %2B dy^2\,$ ,

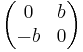which is a quotient map with kernel $\begin{pmatrix}0 & b\\-b & 0\end{pmatrix}$ .

Refinements

An intuitive way to understand an ε-quadratic form is to think of it as a quadratic refinement of its associated ε-symmetric form.

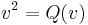For instance, in defining a Clifford algebra over a general field or ring, one quotients the tensor algebra by relations coming from the symmetric form and the quadratic form: $vw%2Bwv=2B(v,w)$ and $v^2=Q(v)$ . If 2 is invertible, this second relation follows from the first (as the quadratic form can be recovered from the associated bilinear form), but at 2 this additional refinement is necessary.

Examples

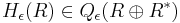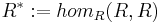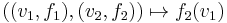An easy example for an ε-quadratic form is the standard hyperbolic ε-quadratic form $H_\epsilon(R) \in Q_\epsilon(R \oplus R^*)$ . (Here, $R^*�:= hom_R(R,R)$ denotes the dual of the $R$ -module $R$ .) It is given by the bilinear form $((v_1,f_1),(v_2,f_2)) \mapsto f_2(v_1)$ . The standard hyperbolic ε-quadratic form is needed for the definition of L-theory.

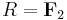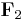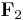For the field of two elements $R={\mathbf F}_2$ there is no difference between (+1)-quadratic and (-1)-quadratic forms, which are just called quadratic forms. The Arf invariant of a nonsingular quadratic form over $\mathbf{F}_2$ is an ${\mathbf F}_2$ -valued invariant with important applications in both algebra and topology.

Given an oriented surface 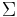$\Sigma$ embedded in 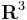$\mathbf{R}^3$ , the middle homology group 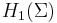$H_1(\Sigma)$ carries not only a skew-symmetric form (via intersection), but also a skew-quadratic form, which can be seen as a quadratic refinement, via self-linking. The skew-symmetric form is an invariant of the surface 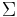$\Sigma$ , whereas the skew-quadratic form is an invariant of the embedding 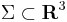$\Sigma \subset \mathbf{R}^3$ , e.g. for the Seifert surface of a knot. The Arf invariant of the skew-quadratic form is a framed cobordism invariant generating the first stable homotopy group $\pi^s_1$ .

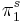For the standard embedded torus, the skew-symmetric form is given by 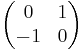$\begin{pmatrix}0 & 1\\-1 & 0\end{pmatrix}$ (with respect to the standard symplectic basis), and the skew-quadratic refinement is given by 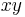$xy$ with respect to this basis: 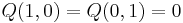$Q(1,0)=Q(0,1)=0$ : the basis curves don't self-link; and 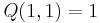$Q(1,1)=1$ : a (1,1) self-links, as in the Hopf fibration. (This form has Arf invariant 0, and thus this embedded torus has Kervaire invariant 0.)

Applications

A key application is in algebraic surgery theory, where even L-groups are defined as Witt groups of ε-quadratic forms, by C.T.C.Wall

References

^ Foundations of algebraic surgery, by Andrew Ranicki, p. 6